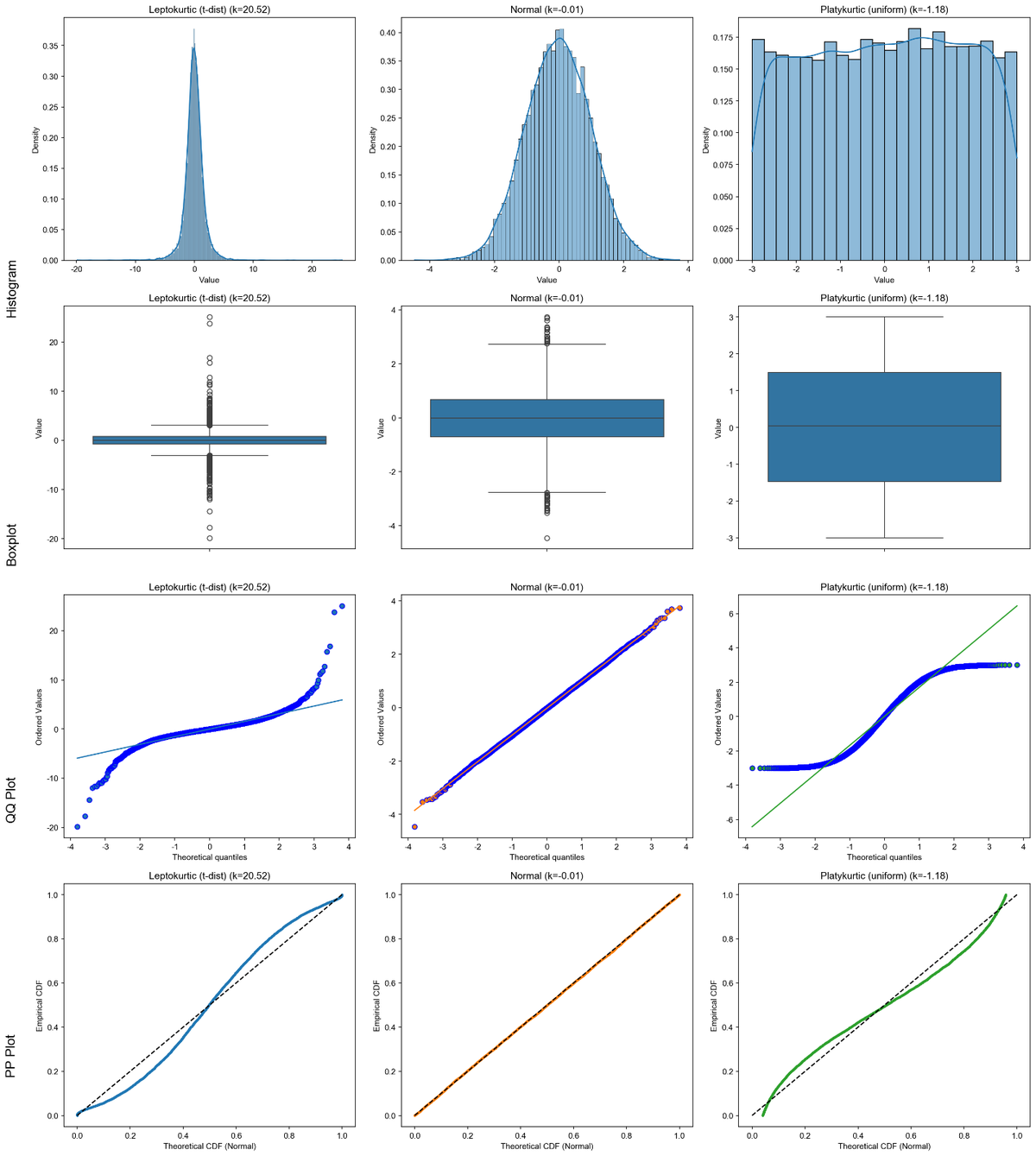
代码如下：

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pandas as pd
import seaborn as sns
from matplotlib.gridspec import GridSpec
import matplotlib as mpl

# 设置支持中文显示（如果您有支持中文的字体）
try:
    plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'SimHei', 'Microsoft YaHei', 'STSong', 'WenQuanYi Micro Hei']
    plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
except:
    pass  # 如果没有合适的中文字体，使用默认字体

# 设置随机种子以保证结果可复现
np.random.seed(42)

# 样本大小
n = 10000

# 生成不同峰度的分布
distributions = {
    'Leptokurtic (t-dist)': stats.t.rvs(df=3, size=n),
    'Normal': np.random.normal(0, 1, n),
    'Platykurtic (uniform)': np.random.uniform(-3, 3, n)
}

# 计算峰度值
for name, data in distributions.items():
    kurtosis = stats.kurtosis(data)
    distributions[name + f' (k={kurtosis:.2f})'] = distributions.pop(name)

# 获取更新后的键名
dist_names = list(distributions.keys())

# 创建一个大图，4行3列
fig, axes = plt.subplots(4, 3, figsize=(18, 20))

# 设置行标题
row_titles = ['Histogram', 'Boxplot', 'QQ Plot', 'PP Plot']

# 1. 直方图 (第一行)
for i, (name, data) in enumerate(distributions.items()):
    sns.histplot(data, kde=True, stat="density", ax=axes[0, i])
    axes[0, i].set_title(f'{name}')
    axes[0, i].set_xlabel('Value')
    axes[0, i].set_ylabel('Density')

# 2. 箱体图 (第二行)
for i, (name, data) in enumerate(distributions.items()):
    sns.boxplot(y=data, ax=axes[1, i])
    axes[1, i].set_title(f'{name}')
    axes[1, i].set_ylabel('Value')
    axes[1, i].set_xlabel('')

# 3. QQ图 (第三行)
for i, (name, data) in enumerate(distributions.items()):
    stats.probplot(data, dist="norm", plot=axes[2, i])
    axes[2, i].set_title(f'{name}')
    axes[2, i].get_lines()[0].set_markerfacecolor(f'C{i}')
    axes[2, i].get_lines()[1].set_color(f'C{i}')

# 4. PP图 (第四行)
for i, (name, data) in enumerate(distributions.items()):
    # 计算经验分位数
    ecdf = np.arange(1, n + 1) / n
    x = np.sort(data)
    # 计算理论分位数 (正态分布)
    norm_cdf = stats.norm.cdf(x, loc=np.mean(data), scale=np.std(data))
    # 绘制PP图
    axes[3, i].scatter(norm_cdf, ecdf, s=3, alpha=0.6, color=f'C{i}')
    axes[3, i].plot([0, 1], [0, 1], 'k--')
    axes[3, i].set_title(f'{name}')
    axes[3, i].set_xlabel('Theoretical CDF (Normal)')
    axes[3, i].set_ylabel('Empirical CDF')

# 添加行标题
for i, title in enumerate(row_titles):
    fig.text(0.02, 0.75 - i*0.22, title, fontsize=16, rotation=90, ha='center', va='center')

plt.tight_layout(rect=[0.03, 0, 1, 1])  # 给左侧留出空间放行标题
plt.savefig('kurtosis_comparison_4x3.png', dpi=150, bbox_inches='tight')
print("图表已保存为 'kurtosis_comparison_4x3.png'")

# 打印峰度统计报告
print("\n峰度统计数据:")
for name, data in distributions.items():
    print(f"{name}:")
    print(f"  均值: {np.mean(data):.4f}")
    print(f"  标准差: {np.std(data):.4f}")
    print(f"  偏度: {stats.skew(data):.4f}")
    print(f"  峰度: {stats.kurtosis(data):.4f}")
    print(f"  25%分位数: {np.percentile(data, 25):.4f}")
    print(f"  中位数: {np.median(data):.4f}")
    print(f"  75%分位数: {np.percentile(data, 75):.4f}")
    print()