Write a class RectangleRulePricer which can price a PathDependentOption using the numerical integration routines written in the earlier exercises. 

Use Equation (A.3) to compute the probability density function for the log of the stock price. Check your solution works with a CallOption.

This gives a numerical test of the derivation of Equation (A.6)

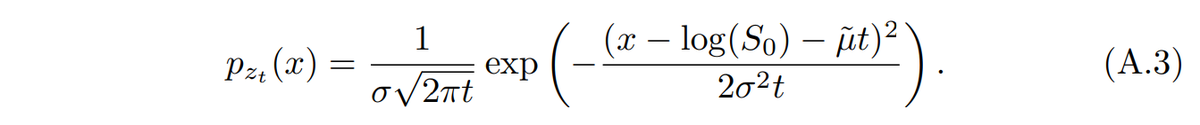
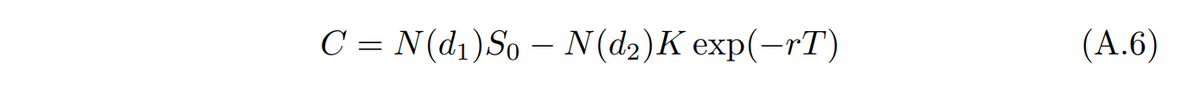
注意：这个题目中的PathDependentOption应该是PathInDependentOption,题目要求存在错误。

找到了书上的答案，copy了一个RectangleRulePricer类实现了这个功能，这个难度相对比较大一些。参考代码：对比视图(17fa4808b46b3a603f38799d1f1d836df14b7532...7742462cae22cb40f572c41d8ba1183e228ead55) · 云金杞/learn_cpp_series - Gitee.com

RectangleRulePricer.h

#pragma once
#include "PathIndependentOption.h"
#include "testing.h"
#include "BlackScholesModel.h"


class RectangleRulePricer {
public:
	int nSteps;
	double price(const PathIndependentOption& option,
		const BlackScholesModel& model);

	RectangleRulePricer() : nSteps(1000) {}
};

void testRectangleRulePricer();

RectangleRulePricer.cpp

#include "RectangleRulePricer.h"

#include "RealFunction.h"
#include "matlib.h"
#include "geometry.h"
#include "CallOption.h"
#include <cmath>

/*
 *  C++11 contains an isfinite function already, but we have
 *  written our own so the code can work on older versions of
 *  Visual Studio
 */
bool isfinitenumber(double arg) {
	return arg == arg &&
		arg != std::numeric_limits<double>::infinity() &&
		arg != -std::numeric_limits<double>::infinity();
}

double RectangleRulePricer::price(const PathIndependentOption& option,
	const BlackScholesModel& model) {



	class ToIntegrate : public RealFunction {
	public:
		const PathIndependentOption& option;
		const BlackScholesModel& model;

		double evaluate(double x) {
			double sigma = model.volatility;
			double muTilde = model.riskFreeRate - 0.5 * sigma * sigma;
			double S0 = model.stockPrice;
			double t = option.getMaturity();

			double probDensity = 1 / (sigma * sqrt(2 * PI * t)) * exp(-pow(x - log(S0) - muTilde * t, 2) / (2 * sigma * sigma * t));
			double payoff = option.payoff(exp(x));
			if (isfinitenumber(payoff)) {
				return payoff * probDensity;
			}
			else {
				// payoffs that can't be evaluated, given
				// the computer's precision are taken to be zero.
				return 0;
			}
		}

		ToIntegrate(const PathIndependentOption& option, const BlackScholesModel& model) :
			option(option), model(model) {}
	};

	ToIntegrate integrand(option, model);

	double expectation = integralOverR(integrand, 1000);
	return exp(-model.riskFreeRate * option.getMaturity()) * expectation;

}

static void testPriceCallOption() {
	BlackScholesModel m;
	m.stockPrice = 100.0;
	m.volatility = 0.1;
	m.drift = 0.0;
	m.riskFreeRate = 0.1;
	CallOption c;
	c.setStrike(100.0);
	c.setMaturity(2.0);
	double expected = c.price(m);
	RectangleRulePricer pricer;
	double actual = pricer.price(c, m);
	ASSERT_APPROX_EQUAL(actual, expected, 0.01);
}


void testRectangleRulePricer() {
	TEST(testPriceCallOption);
}